
Proof by Contradiction
关于抬杠的哲学
本文作者
范智渊
Franky
香港中文大学
电子信息工程专业
主授:A-level, IG, IB, AP 物理&数学;择校数学
个人特色:
丰富的教学经验,熟悉各种体系物理和数学科目。
性格活泼开朗,课堂氛围轻松愉快,喜爱使用生动例子解释抽象内容,帮助加深学生理解;
擅长总结高效学习方法来解决数学、物理学习中的难点。
When you have eliminated all which is impossible, then whatever remains, however improbable, must be the truth.
Proof by contradiction,让复习Edexcel P4的同学们会有一些抓狂。绕来绕去不清楚。相比较从逻辑上反推结论,直接用公式定理证出:
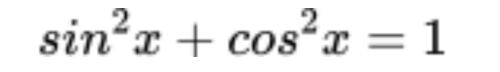
让同学们感觉更干脆利落。但事实上,我常跟学生讲,如果你能想清楚Proof by contradiction背后的逻辑,或许你能感受到一些数学的力量和美。
01
理解Proof by contradiction
我们需要先理解归谬
为了理解Proof by contradiction,我们需要先理解归谬,拉丁语:reductio ad absurdum,我们先举一个不那么精确的例子:
张三声明:我研发了一个无敌围棋AI,能确保无论对手是谁,都一定能赢。
数学老师:如果让两个无敌围棋AI对弈,根据张三的论述,执黑一定会赢,执白一定会赢。围棋规定只有一个赢家。矛盾产生,原命题错误。
谬误与矛盾,是Proof by contradiction的根本。
当你想证明“A”为真,你可以假设 “A的反面”为真。通过证明“A的反面”为假,证明“A”为真。“A”和“A的反面”必然一真一假。
这个道理很好理解,你不可能投出一枚硬币,正面反面都朝上。那么在P4考试中应对所有的题目,难点都在于如何找到“反面”从而推理出矛盾。
02
两个简单的例题
大致理解Proof by contradict答题技巧
01

题目意思是:对于所有的偶数n,n3, 都是偶数。
那么这句话的反面应该是:存在一个奇数n,n3偶数。假设这句话为真。转成数学的语言:
which is not even
我们证明对于所有的奇数,假设都不成立。如果假设不成立原始的命题就必然成立。
02

此题需要我们证明:没有最大的奇整数。我们找到“反面”:假设,有最大的奇整数。翻译成数学语言:
存在一个最大的奇整数n=2k+1,那么n+2=2k+3也是一个奇数,并且很明显n+2>n
这个例题中,我们从n 是最大奇整数出发,通过简单的逻辑推导出n不是最大奇整数的矛盾。通过假设是错误的证明:不存在最大奇整数。
通过这两个简单的例题,我们大致能够理解Proof by contradict的答题技巧:
1直接假设题目的“反面”是真的。
2以此为基础,进行推理,(记住目标是找到谬误或者矛盾)。
3找到矛盾,题目得证。
而在一些具体的题目中,“反面”可能存在多种情况。这时候,记住开篇的那句话:“排除掉所有不可能,剩下的,再奇怪也是真相”。
理解Proof by contradiction,不仅能帮助同学们在考试中拿分。对于同学们思考现实问题、谨防上当受骗、甚至网络对线(当然不建议大家上网对线)都极有裨益。
最后用一个简单的命题结束本篇:如果你看到这里,你一定非常热爱数学。alevel详情咨询老师即可~

