alevel数学：利润常数还是自然常数？

　　alevel数学：利润常数还是自然常数？大家在学习数学时会碰到很多比较奇怪又让人难以理解的“常数”，自然常数e应该是首当其冲了，相比于同样是无理数的来说，它更让人捉摸不透。对于，大家都比较熟悉，就是圆周率，是圆的周长与圆半径的比值。那么自然常数e到底是什么，它是怎么来的，今天我们就简单的来818。

　　利润常数

　　最早与e有关的发现是在1618年，由John Napier提出的对数表中，有涉及到与自然常数e相关的计算结果，但当时他并没有意识这个常数的存在。

　　自然常数e真正的发现是在1683年，由Jacob Bernoulli在做和复利（compound interest）相关的计算时发现的。

　　它的定义就是：

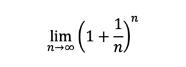
　　当时他所研究的问题就是：

　　如果我有1块钱，我们都知道在年利率是100%的情况下，用单利计算得到的本金+利润是：

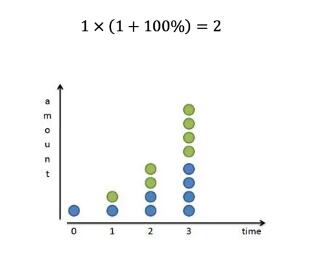
　　但是，如果我们把单利改成复利，得到的钱就会增加，比如存半年，拿出来，再存半年，那我们可以得到的钱就会变成：

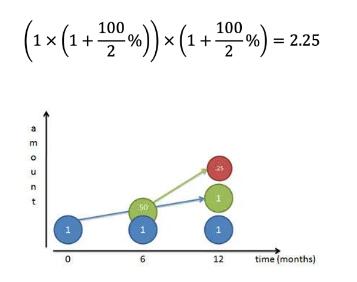
　　那不断的增加我存取的次数，从半年存取一次，到每季度，到每个月，到每天，甚至到最后的每时每刻，我们最后得到的本金+利润是否会无限大呢？

　　很多人就是这么猜想的，但根据Jacob Bernoulli计算出来的结果却是相反的，他发现最后我们的本金+利润会趋于一个常数，这个常数的数值大概是2.7182818...，也就是我们现在的自然常数e。

　　所以，自然常数e就是一个本利常数。（那干嘛叫自然常数呢？

　　自然常数

　　因为它真的在自然界中无处不在！

　　比如之前老师有给大家介绍过的硬核的数学图腾——螺旋线，在自然界中也是随处可见，其中就有涉及到自然常数e的出现，

　　以及近年比较火的泼水成冰，看看这优美的弧线，是不是很眼熟？

　　对就是它了，对数螺旋线，在极坐标下，它的方程是：

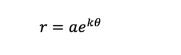
　　在之前有一期讲到的放射性物质的衰变时会有一个“半衰期”的概念，其实也是因为它的衰变方程与自然常数有关。

　　最后，让我们来看看被无数数学家们誉为最美数学公式的上帝公式（欧拉公式）：

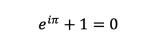
　　这是一个囊括了数学中实数的基本单位、虚数的基本单位、0、两个最最特殊的无理数，并且只用了最简单的加法去连接他们的一个公式。