四个步骤轻松解决AP微积分中的微分应用题型?

　　四个步骤轻松解决AP微积分中的微分应用题型?

　　在AP微积分中，一类很常见的应用题就是Related Rates（相关变化率），这类习题因为各种不同的场景，变化比较多，已知条件也比较复杂，很多同学在做这类习题时都感觉没什么头绪，今天给大家总结一下这类习题的解题思路。

　　我们先看一道例题：

　　1.题目分析：

　　这道题中，半径的变化是恒定的，但是面积的变化不恒定，我们需要找到面积和半径的恒等关系，因为半径和面积都是随着时间在变化，所以需要对面积和半径关系的恒等式进行相对于时间的微分。

　　2.解题过程：

　　3.思路总结：

　　这类习题其实是有固定的解题步骤的，在此我们为大家总结一下：

　　1.找到所有的已知量和未知量，其中会有两个关于变化率的变量，一个是已知，一个是未知，例如本题中的半径和面积。

　　2. 我们需要找到两个变量的恒等关系，这类恒等关系一般可以通过以下几种关系来找到：面积关系、体积关系、三角函数关系、勾股定理关系和比例关系。

　　3.列出恒定关系后，针对方程两边，同时相对于时间t做微分。

　　4.代入已知数值，求解。

　　相关变化率的场景可能有各种变化，但是解题步骤是不变的，我们再来看一道例题：

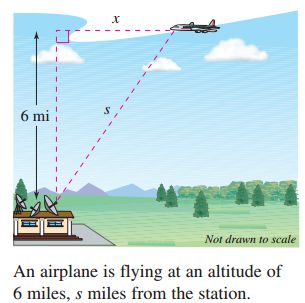
　　本题中，已知的是s相对于时间的变化率，未知的是x相对于时间的变化率，根据我们的总结，此题我们可以根据s和x的勾股定理关系，找到变化率的关系，解题过程如下：

　　今天的知识点答题思路分享就到这里，总而言之，相关变化率的场景可能有各种变化，但是解题步骤是不变的，同学们遇到此类题型，按照我们今天分享的步骤作答就OK了。