1.离散分布(discrete distribution)︰如果random variable(随机变量)X只能取某些特定的数值,那么X对应的分布为离散分布。在a level考试里常见的情况就是只能取整数,如∶人数、物品个数、事件发生次数等。以下为必考的经典离散分布:
1.) binomial distribution(二项分布)∶
x~B(n,p)
用于描述在n次相互独立的实验中,实验成功的次数。其中p为成功的概率,如10次抛硬币的实验中,正面朝上的次数。
2.) poisson distribution(泊松分布)
x~poi(入)
用于描述单位时间内,指定的随机事件发生的次数,如某一服务设施在一定时间内到达的人数,电话接到呼叫的次数,汽车站台的候客人数,机器出现的故障数,自然灾害发生的次数等等。
2.连续分布(continuous distribution)︰一个随机变量x,在其区间内当能够取任何数值时所具有的分布。
相比离散分布,连续分布的模型更加抽象,需要从frequency function(密度曲线)的角度去理解和记忆该分布的知识点。
1) normal distribution(正态分布): 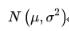
Frequency function图像特征: mode、mean和median都集中在同一个x的取值上,同时图像的peak也出现在这一点上。是一条bell-curve。
所以由图像特征可推出,对于一个服从normal distribution的random variable而言,x的取值发生在mean附近概率是最大的。偏离mean越多,相应事件发生的概率会越小。
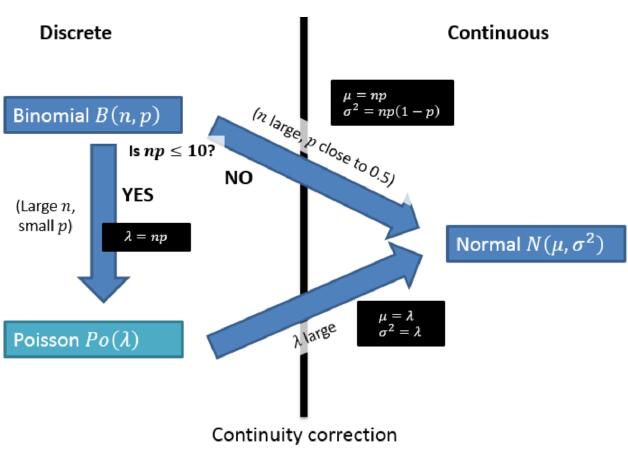
考试中formula sheet会有binomial distribution和poisson distribution的cumulative distribution function的表格,但如果题目里poisson distribution的入超过10,binomial distribution的n超过了40 等无法从表格直接看出来cumulative probability的情况我们该怎么办呢?
normal distribution就能帮我们解决这个问题! binomial distribution和poisson distribution都能近似于normal distribution,那什么情况下可以做这样的approximation呢?我们总结出了以下的关系。