A-level数学积分法则

　　A-level数学积分法则

　　对于A-level数学的Pure Math部分来说，难度最高也最复杂的部分应该就是积分了，很多同学在做积分的时候经常分不清什么时候该用哪个公式，今天我们带大家来一起总结一下。

　　一、基本公式

　　首先要知道积分法则是微分法则的逆运算，所以基本的公式如下：

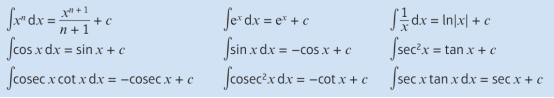
　　这部分的公式全是由微分的公式倒推出来的，而且公式表上是没有的，所以一定要记牢。

　　二、反链式法则

　　接下来是反链式法则（Reverse Chain Rule），也就是说，如果上面的基本公式中，x的位置被（ax+b）的形式替换，那么我们把积分结果的式子中的x也整体替换成（ax+b），然后再除以a即可。

　　注意！这个只限定x被一个一次函数的式子（ax+b）替换，其他时候是不行的哦。

　　三、两种嵌套形式

　　如果遇到分子是分母的微分，结果就是ln的表达式；如果式子中是函数的n次幂再乘函数的微分，结果是函数的n+1次幂之后再除以n+1。

　　这种嵌套形式有的同学在做题时可能看不出来，但其实没关系，用代入法Substitution一样能做出来。让u=f（x）就可以。

　　四、代入积分法Substitution

　　请看一道例题：

　　代入法的关键是找到u，并把dx替换成du的表达式。

　　五、分部积分法Integration by Parts

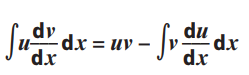
　　分部积分法的关键是确定好表达式中哪部分是u，哪部分是dv/dx，这里我们的原则是，u的部分做完微分之后要变得更简单，dv/dx的部分我们要会做积分。这里有一个小窍门，如果式子里有lnx，那么lnx是u；如果没有，那么x的n次幂是u。

　　六、裂项积分法（Partial Fraction）

　　对于复杂的分式，我们不能直接做积分，需要拆成好几项。常见的三种情况如下：

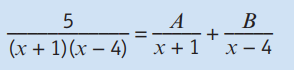
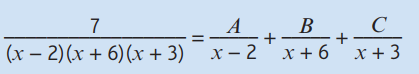
　　拆成分式之后，就可以分别的做积分了。

　　除了基本公式之外，很多同学分不清什么时候用代入法，什么时候用分部法，这里最后给大家一个诀窍：如果是相同类型函数（比如都是多项式函数或是三角函数）相乘除，那么用代入积分法；如果是不同类型函数相乘（比如x和sinx；x和lnx），用分部积分法。